What Is 3/4 In Half
mumtaazwhitefield
Sep 11, 2025 · 6 min read
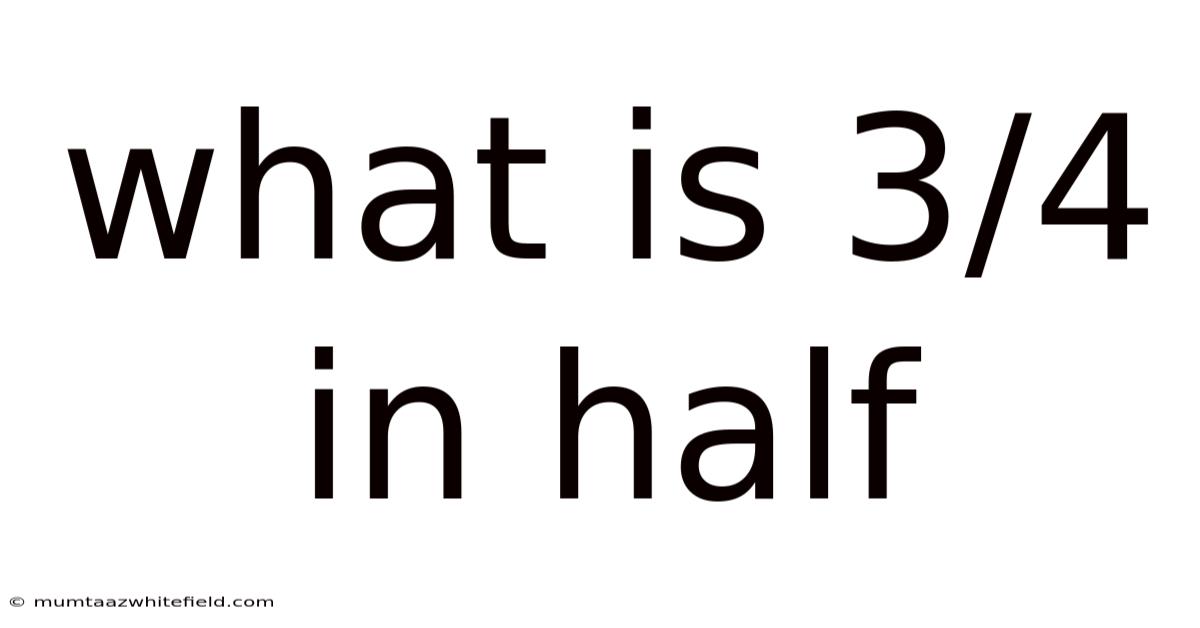
Table of Contents
What is 3/4 in Half? Unpacking Fractions and Division
Understanding fractions can sometimes feel like navigating a maze, especially when we introduce further operations like division. This article will comprehensively explore the question: "What is 3/4 in half?" We'll break down the process step-by-step, providing a clear understanding not just of the answer but also of the underlying mathematical principles involved. This explanation is designed for anyone, from those just starting to grasp fractions to those looking to refresh their understanding of fractional arithmetic. We'll delve into the practical applications, explore different methods of solving this problem, and address common misconceptions.
Understanding Fractions: A Quick Refresher
Before we dive into dividing 3/4 in half, let's briefly review the fundamental concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts of a whole.
Method 1: Dividing by 2 (Multiplying by 1/2)
The most straightforward approach to finding half of 3/4 is to divide it by 2. Remember, dividing by a number is the same as multiplying by its reciprocal. The reciprocal of 2 is 1/2. Therefore, we can rewrite the problem as:
(3/4) ÷ 2 = (3/4) × (1/2)
To multiply fractions, we simply multiply the numerators together and the denominators together:
(3 × 1) / (4 × 2) = 3/8
Therefore, half of 3/4 is 3/8.
Method 2: Visual Representation
Visualizing the problem can often make abstract concepts more concrete. Imagine a pizza cut into four equal slices. 3/4 of the pizza represents three of these slices. To find half of 3/4, we need to divide those three slices in half. This would result in six smaller slices, where each smaller slice represents 1/8 of the whole pizza. Therefore, half of 3/4 is 3/8. This visual method reinforces the numerical result obtained through calculation.
Method 3: Converting to Decimals
Another approach involves converting the fraction 3/4 into its decimal equivalent before dividing. To do this, we divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Now, we can divide the decimal by 2:
0.75 ÷ 2 = 0.375
Finally, we can convert the decimal back into a fraction. 0.375 can be expressed as 375/1000. Simplifying this fraction by dividing both the numerator and the denominator by their greatest common divisor (125) gives us:
375/1000 = 3/8
Again, this confirms that half of 3/4 is 3/8.
Understanding the Relationship: Halving and Doubling
It's important to understand the inverse relationship between halving and doubling. If half of 3/4 is 3/8, then doubling 3/8 should give us back 3/4. Let's check:
3/8 × 2 = (3 × 2) / 8 = 6/8
Simplifying 6/8 by dividing both the numerator and denominator by 2, we get 3/4. This demonstrates the consistency and accuracy of our calculations.
Practical Applications: Real-World Examples
Understanding how to divide fractions is crucial in many everyday situations. Here are a few examples:
- Cooking: If a recipe calls for 3/4 of a cup of flour, and you want to halve the recipe, you would need 3/8 of a cup of flour.
- Sewing: If a pattern requires 3/4 of a yard of fabric, and you only want to make half the project, you'll need 3/8 of a yard.
- Construction: If a project requires 3/4 of a gallon of paint, and you need to complete only half the job, you'll need 3/8 of a gallon.
These scenarios illustrate the practical relevance of understanding fractional division in everyday life.
Addressing Common Misconceptions
One common mistake is to simply halve the numerator while leaving the denominator unchanged. This would incorrectly result in 3/2 (or 1 1/2), which is not half of 3/4. Remember, when dividing a fraction, we divide both the numerator and the denominator, or, more accurately, we multiply by the reciprocal.
Another misconception involves confusing division with subtraction. Dividing 3/4 by 2 is not the same as subtracting 1/2 from 3/4. These are distinct mathematical operations yielding different results. Subtracting 1/2 from 3/4 would involve finding a common denominator and then subtracting the numerators, resulting in 1/4.
Further Exploration: More Complex Fractional Divisions
The principles discussed here can be extended to more complex fractional division problems. For instance, finding one-third of 3/4 would involve dividing 3/4 by 3 (or multiplying by 1/3). Similarly, finding a quarter of 3/4 would involve dividing 3/4 by 4 (or multiplying by 1/4). The same principles of multiplying numerators and denominators apply.
Mastering fractional division is essential for a solid understanding of mathematics. It lays the foundation for more advanced concepts in algebra, calculus, and other mathematical disciplines.
Frequently Asked Questions (FAQ)
Q: Can I divide the numerator and denominator separately to find half of 3/4?
A: While it seems intuitive to halve both the numerator and the denominator, this is not mathematically correct. The correct method is to multiply 3/4 by 1/2, resulting in 3/8.
Q: Why is it important to simplify fractions?
A: Simplifying fractions helps to present the answer in its most concise and easily understandable form. It also makes further calculations simpler and more efficient.
Q: What if I wanted to find a different fraction of 3/4, say, one-fifth?
A: To find one-fifth of 3/4, you would multiply 3/4 by 1/5, which is (3 x 1) / (4 x 5) = 3/20.
Conclusion: Mastering Fractional Division
Finding half of 3/4, or any fraction for that matter, is a fundamental skill in mathematics. This article has explored three different methods to arrive at the correct answer: 3/8. We have emphasized the importance of understanding the underlying principles of fractions, the significance of reciprocal multiplication, and the utility of visual representations. By understanding these concepts, you'll be well-equipped to tackle more complex fractional calculations and apply them to real-world problems. Remember, practice is key to mastering any mathematical skill, so don't hesitate to work through more examples to build your confidence and expertise. The world of fractions may seem initially daunting, but with persistent effort and a clear understanding of the underlying principles, you can navigate it with ease and confidence.
Latest Posts
Latest Posts
-
How To Lose 15 Kilos
Sep 11, 2025
-
14 Inch Laptop I7 Processor
Sep 11, 2025
-
Pornstar With The Biggest Butt
Sep 11, 2025
-
Best Coffee In Richmond Va
Sep 11, 2025
-
Anime Chicks With Big Boobs
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 In Half . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.