Half Of 2 1 2
mumtaazwhitefield
Sep 11, 2025 · 6 min read
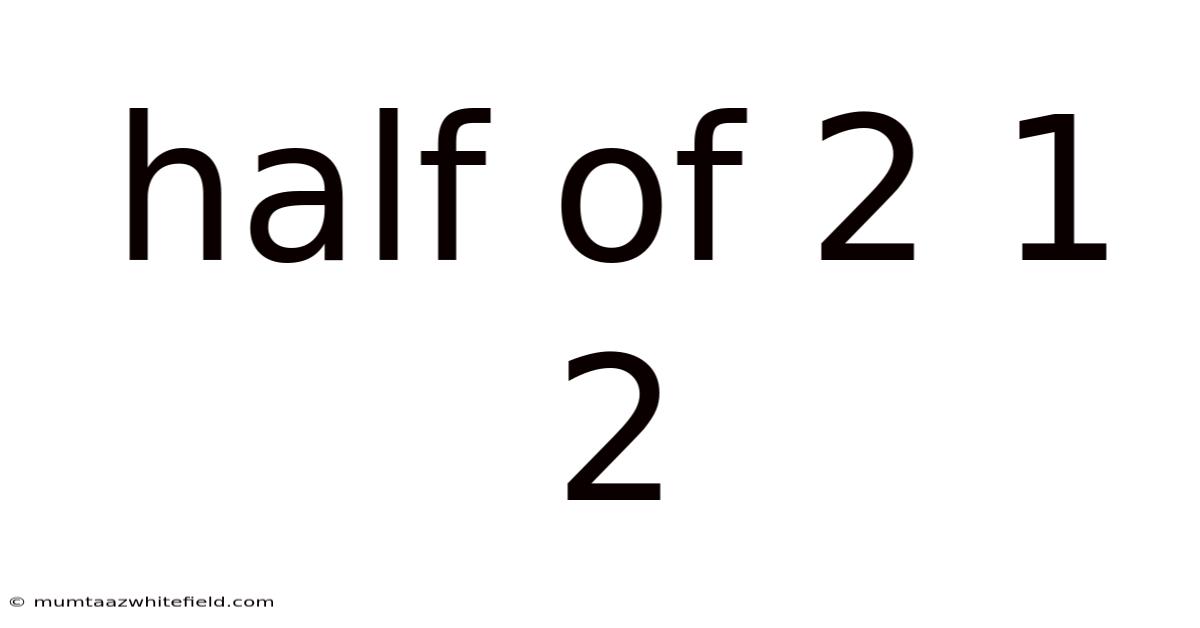
Table of Contents
Decoding "Half of 2 1 2": Exploring Mathematical Concepts and Problem-Solving Strategies
What is half of 2 1 2? This seemingly simple question opens a door to a fascinating exploration of mathematical concepts, from basic arithmetic to the nuances of interpreting ambiguous notation. Understanding how to approach this problem requires careful consideration of several factors, and mastering these factors enhances our overall mathematical literacy. This article delves deep into the possible interpretations and solutions, emphasizing the importance of clear communication and precise mathematical language.
Introduction: The Importance of Clarity in Mathematics
At first glance, "half of 2 1 2" seems straightforward. However, the lack of explicit operators between the numbers introduces ambiguity. This ambiguity highlights the critical importance of precise notation in mathematics. A small change in how a problem is written can dramatically alter its meaning and the resulting answer. This problem serves as an excellent example of why mathematicians stress the use of unambiguous notation and clear definitions.
Interpretation 1: Treating "2 1 2" as a Single Number
One interpretation of "2 1 2" is to treat it as a single, three-digit number: two hundred and twelve. In this case, the problem becomes: "What is half of 212?".
Calculation:
To solve this, we perform a simple division: 212 / 2 = 106
Therefore, under this interpretation, half of 2 1 2 is 106. This is the most straightforward and likely intended interpretation if the question was posed informally.
Interpretation 2: Considering "2 1 2" as a Concatenated Expression
Another interpretation involves treating "2 1 2" as a concatenation of three separate numbers: 2, 1, and 2. However, this interpretation requires further clarification regarding the intended operation. Several possibilities exist:
-
Scenario A: Summation: We could interpret it as finding the sum of 2, 1, and 2 (2 + 1 + 2 = 5) and then finding half of the result.
Calculation:
(2 + 1 + 2) / 2 = 5 / 2 = 2.5
In this scenario, half of 2 1 2 is 2.5.
-
Scenario B: Multiplication: Alternatively, we could interpret it as finding the product of 2, 1, and 2 (2 * 1 * 2 = 4) and then finding half of the result.
Calculation:
(2 * 1 * 2) / 2 = 4 / 2 = 2
Here, half of 2 1 2 is 2.
-
Scenario C: Sequence of Operations: We could interpret this as a sequence of operations, but without specified operators, this becomes highly speculative. This highlights the need for mathematical operators such as +, -, ×, ÷, to clarify intended operations. Without these, any interpretation is merely conjecture.
Interpretation 3: Base Number Systems
For those familiar with different base number systems, "2 1 2" could be interpreted in a non-decimal system. However, without specification of the base, any such interpretation would be purely speculative. For instance:
-
Base 3: In base 3, "2 1 2" would represent (2 * 3²) + (1 * 3¹) + (2 * 3⁰) = 18 + 3 + 2 = 23. Half of 23 is 11.5.
-
Base 4: In base 4, "2 1 2" would represent (2 * 4²) + (1 * 4¹) + (2 * 4⁰) = 32 + 4 + 2 = 38. Half of 38 is 19.
This illustrates the significant impact that context and underlying assumptions can have on mathematical interpretation. Without knowing the intended base, this interpretation is impractical.
The Importance of Precise Mathematical Notation
The ambiguity surrounding "half of 2 1 2" underscores the importance of precise mathematical notation. Mathematical language is designed to eliminate ambiguity and ensure that everyone understands the problem in the same way. Using standard mathematical notation, like parentheses and explicit operators, would eliminate any doubt. For example:
- "(2 + 1 + 2) / 2" clearly indicates the sum of 2, 1, and 2, divided by 2.
- "(2 * 1 * 2) / 2" unambiguously shows the product of 2, 1, and 2, divided by 2.
- "212 / 2" directly expresses half of two hundred and twelve.
The use of consistent and clear notation is crucial for effective communication and problem-solving in mathematics and beyond. Ambiguous expressions can lead to errors, confusion, and misunderstandings.
Problem-Solving Strategies and Mathematical Thinking
This seemingly simple problem highlights the critical thinking skills necessary for successful problem-solving in mathematics:
- Identify the ambiguity: The first step is to recognize the potential for multiple interpretations of the problem.
- Consider all possibilities: Explore all reasonable ways to interpret the ambiguous notation.
- Justify your approach: Clearly explain the rationale behind the chosen interpretation and the steps taken to solve the problem.
- Communicate effectively: Present your solution in a clear and concise manner, ensuring the reader understands your reasoning.
These problem-solving skills are transferable to many areas, including science, engineering, and even everyday life. The ability to break down complex problems into smaller, manageable parts and to consider alternative solutions is crucial for effective problem-solving.
Expanding on Mathematical Concepts
This seemingly simple problem touches upon several important mathematical concepts:
- Arithmetic Operations: The problem involves basic arithmetic operations like addition, multiplication, and division.
- Order of Operations: The lack of explicit operators necessitates consideration of the order of operations (PEMDAS/BODMAS), although in this case, it’s less directly applicable due to the ambiguity.
- Number Systems: The exploration of different base number systems expands our understanding of how numbers can be represented.
- Ambiguity and Precision: The problem highlights the crucial role of precise mathematical language in avoiding ambiguity and ensuring clear communication.
Frequently Asked Questions (FAQ)
-
Q: What is the correct answer to "half of 2 1 2"?
- A: There is no single "correct" answer without further clarification of the intended meaning of "2 1 2". The answer depends entirely on the interpretation of the notation.
-
Q: Why is this problem so ambiguous?
- A: The ambiguity stems from the absence of explicit operators (+, -, ×, ÷) between the numbers. This lack of clarity allows for multiple interpretations.
-
Q: How can I avoid this type of ambiguity in my own work?
- A: Always use clear and unambiguous mathematical notation. Use parentheses to group terms, and explicitly state the operations to be performed.
-
Q: Is this a trick question?
- A: It's not necessarily a "trick" question, but it is a cleverly designed problem that highlights the importance of precision and clear communication in mathematics.
Conclusion: The Value of Mathematical Precision
The exploration of "half of 2 1 2" is more than just a simple arithmetic exercise. It's a valuable lesson in the importance of precise mathematical notation, clear communication, and critical thinking. Understanding the potential for ambiguity and practicing careful interpretation strengthens mathematical skills and promotes clearer problem-solving strategies. The seemingly simple question unveils a wealth of mathematical concepts and highlights the necessity for precision in all aspects of mathematical work. This exercise emphasizes that mathematical understanding is not merely about arriving at a numerical answer but also about comprehending the underlying concepts and reasoning involved. The ability to navigate ambiguity and arrive at well-justified solutions is a crucial skill in all areas where mathematics plays a role.
Latest Posts
Latest Posts
-
Black Trousers And White Shirt
Sep 11, 2025
-
Towel Rack That Dries Towels
Sep 11, 2025
-
What Is This In Japanese
Sep 11, 2025
-
Which Is The Gay Earring
Sep 11, 2025
-
Blonde And Brown Hair Dye
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Half Of 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.