Differentiate X 1 X 1
mumtaazwhitefield
Sep 15, 2025 · 5 min read
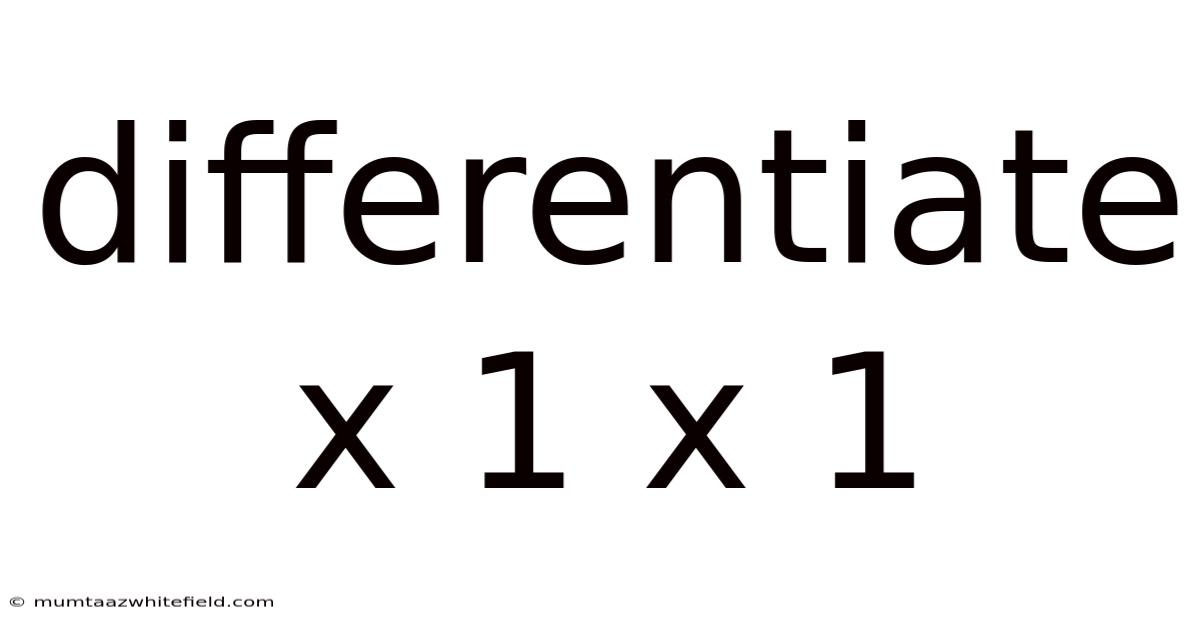
Table of Contents
Differentiate x¹ˣ¹
The expression "x¹ˣ¹," while seemingly simple, presents a significant challenge in differentiation because the exponent itself is a function of x. This isn't a straightforward application of the power rule; instead, it requires a deeper understanding of logarithmic differentiation and the chain rule. This article will delve into the intricacies of differentiating this expression, explaining the process step-by-step and providing a thorough understanding of the underlying mathematical principles. We'll also address common misconceptions and explore related concepts.
Understanding the Challenge: Why the Power Rule Fails
Before we begin the differentiation process, let's clarify why the basic power rule, which states that the derivative of xⁿ is nxⁿ⁻¹, cannot be directly applied here. The power rule applies when the exponent is a constant. In x¹ˣ¹, the exponent (1ˣ) is a variable expression, making the power rule inapplicable. We need a more sophisticated approach.
Step-by-Step Differentiation using Logarithmic Differentiation
Logarithmic differentiation provides an elegant solution to differentiating functions with variable exponents. Here's how we tackle x¹ˣ¹:
1. Take the Natural Logarithm of Both Sides:
Let y = x¹ˣ¹. Taking the natural logarithm (ln) of both sides, we get:
ln(y) = ln(x¹ˣ¹)
2. Apply the Power Rule of Logarithms:
Using the property of logarithms that ln(aᵇ) = b * ln(a), we can simplify the right-hand side:
ln(y) = x¹ * ln(x) = x ln(x)
3. Implicit Differentiation:
Now, we differentiate both sides of the equation with respect to x. Remember that we are performing implicit differentiation since y is a function of x. The derivative of ln(y) with respect to x is (1/y) * (dy/dx) using the chain rule. The derivative of x ln(x) requires the product rule.
d/dx [ln(y)] = d/dx [x ln(x)]
(1/y) * (dy/dx) = x * (1/x) + ln(x) * 1
(1/y) * (dy/dx) = 1 + ln(x)
4. Solve for dy/dx:
To isolate dy/dx (which represents the derivative of y with respect to x), multiply both sides by y:
dy/dx = y * (1 + ln(x))
5. Substitute the Original Expression for y:
Finally, substitute the original expression for y (y = x¹ˣ¹) back into the equation:
dy/dx = x¹ˣ¹ * (1 + ln(x))
Therefore, the derivative of x¹ˣ¹ is x¹ˣ¹ * (1 + ln(x)).
A Deeper Dive into the Mathematical Concepts
Let's examine the key mathematical principles employed in the above derivation:
-
Logarithmic Differentiation: This technique is particularly useful for differentiating complex functions, especially those involving variable exponents or products of multiple functions. By taking the logarithm of both sides, we transform the problem into a simpler form that can be differentiated using more elementary rules.
-
The Chain Rule: The chain rule is crucial in calculus. It states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) times the derivative of the inner function. In our case, the chain rule was applied when differentiating ln(y) with respect to x.
-
The Product Rule: The product rule is essential when differentiating a product of two functions. It states that the derivative of a product is the first function times the derivative of the second function plus the second function times the derivative of the first function. We applied this rule when differentiating x ln(x).
-
Implicit Differentiation: When we have an equation where y is not explicitly defined as a function of x, we use implicit differentiation. This technique involves differentiating both sides of the equation with respect to x, treating y as a function of x and applying the chain rule as needed.
Addressing Common Misconceptions
Several common misunderstandings can arise when tackling this type of problem:
-
Incorrect Application of the Power Rule: The most frequent error is attempting to apply the power rule directly. It’s crucial to remember that the power rule is only valid for constant exponents.
-
Forgetting the Chain Rule: The chain rule is essential in logarithmic differentiation and is often overlooked, leading to incomplete or incorrect derivatives.
-
Neglecting the Product Rule: When using logarithmic differentiation, functions often become products, necessitating the correct application of the product rule.
Extending the Understanding: Related Concepts
The techniques used to differentiate x¹ˣ¹ are applicable to a broader class of functions with variable exponents. For example, consider the function f(x) = xˣ. The same logarithmic differentiation technique can be employed to find its derivative, which is found to be xˣ(1 + ln(x)). This illustrates the general applicability of this powerful method.
Furthermore, understanding logarithmic differentiation opens doors to tackling even more complex scenarios involving exponential functions with variable bases and exponents, fractional exponents, and more intricate combinations of functions.
Frequently Asked Questions (FAQ)
-
Q: Can I use other bases besides the natural logarithm (ln)? A: While the natural logarithm is often preferred for its simplicity in differentiation, you can use other logarithmic bases (e.g., log₁₀). However, remember to adjust the derivative accordingly using the change of base formula.
-
Q: What if the exponent were more complicated? A: The same principles apply even with more complex exponents. The key is to carefully apply the chain rule and product rule as needed. For example, if the exponent was x² + 2x, the derivative would involve additional steps, but the fundamental approach remains the same.
-
Q: Are there other methods to differentiate x¹ˣ¹? A: While logarithmic differentiation is the most efficient and commonly used method, there are other approaches that could be employed, but they tend to be more complex and less straightforward.
-
Q: What are the applications of this type of differentiation? A: Differentiating functions with variable exponents finds applications in various fields, including physics (modeling exponential growth and decay), economics (compound interest calculations), and engineering (solving differential equations related to complex systems).
Conclusion
Differentiating x¹ˣ¹ is not a trivial task, but by employing logarithmic differentiation in combination with the chain and product rules, we can successfully derive its derivative: x¹ˣ¹ * (1 + ln(x)). This detailed explanation should equip you with the necessary knowledge and understanding not only to solve this specific problem but also to tackle similar challenges involving functions with variable exponents. The key takeaway is to appreciate the power and elegance of logarithmic differentiation as a tool in your calculus arsenal. Mastering these concepts opens up a vast landscape of mathematical possibilities. Remember that practice is crucial to solidifying your understanding and building confidence in tackling increasingly complex differentiation problems.
Latest Posts
Latest Posts
-
Why Poodles Are The Worst
Sep 15, 2025
-
How Many Hours In A Year
Sep 15, 2025
-
Black Shirt With Navy Pants
Sep 15, 2025
-
Dark Hair With Ash Blonde
Sep 15, 2025
-
Is Weed Legal In Canberra
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Differentiate X 1 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.