3 4 In 1 2
mumtaazwhitefield
Sep 12, 2025 · 6 min read
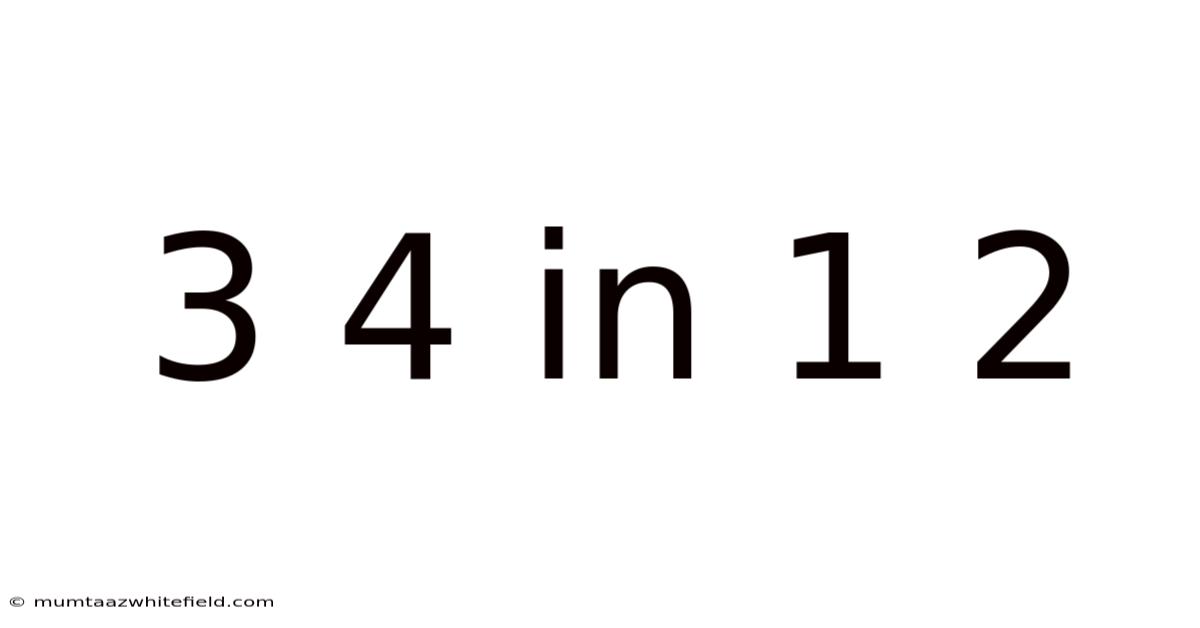
Table of Contents
Decoding the Mathematical Enigma: 3, 4, in 1, 2
This article delves into the fascinating world of mathematical patterns and logic puzzles, specifically focusing on the seemingly simple, yet surprisingly complex, sequence: 3, 4, in 1, 2. This sequence, while not a standard mathematical progression, invites us to explore various interpretations and problem-solving approaches. We will examine different perspectives, explore potential solutions, and ultimately, demonstrate the power of creative thinking in deciphering cryptic sequences. Understanding this puzzle helps develop critical thinking skills applicable to various fields, from coding to cryptography.
Understanding the Puzzle: The Ambiguity of "in"
The core challenge lies in the word "in." It acts as a crucial, yet ambiguous, element. Unlike numerical operators (+, -, ×, ÷), "in" doesn't have a clearly defined mathematical meaning in this context. This ambiguity opens up a range of possibilities, demanding creative interpretations. We'll explore several approaches, each justified by different logical frameworks.
Approach 1: Interpreting "in" as a Positional Indicator
One interpretation views "in" as indicating the position of a number within a larger sequence or set. Let's assume the sequence continues. We could imagine a scenario where "in 1, 2" specifies that the numbers 1 and 2 are situated within a larger sequence, perhaps influencing the next numbers in the pattern. This approach encourages us to think beyond the immediately presented sequence and consider its potential continuation.
This positional approach could lead us to explore different potential continuations. For instance, if we assume a cyclical pattern, the next numbers might be 3, 4, ... repeating the sequence. However, without further information, this remains speculative. This approach highlights the importance of context in mathematical problem-solving. The absence of context allows for multiple interpretations, each with its own logic.
Furthermore, we can explore variations on this positional theme. Perhaps "in 1, 2" refers to a specific position within a larger system, such as a coordinate plane or a matrix. In this scenario, we would need additional information to pinpoint the exact location and its significance to the overall sequence. This interpretive flexibility is a hallmark of such puzzles and emphasizes the importance of lateral thinking.
Approach 2: "in" as a Relational Operator
Another approach involves interpreting "in" as a relational operator, suggesting a relationship between the numbers 3, 4 and the pair 1, 2. This could involve various mathematical relationships:
-
Difference: The difference between 3 and 4 is 1, and the difference between 2 and 1 is also 1. This could suggest a constant difference as a defining characteristic of the pattern.
-
Ratio: The ratio between 3 and 4 is approximately 0.75. The ratio between 2 and 1 is 2. While no obvious pattern emerges from these ratios alone, it's a potential avenue of exploration.
-
Modular Arithmetic: We can explore the remainders when numbers are divided by certain moduli. For example, 3 mod 2 = 1 and 4 mod 2 = 0. Similarly, 1 mod 2 = 1 and 2 mod 2 = 0. While this yields a certain symmetry, it does not fully elucidate the sequence’s underlying rule.
-
Combination: A more complex relationship might involve a combination of these operations. For example, the difference between the numbers could be related to their position in the sequence or their modular arithmetic properties.
The exploration of relational operators highlights the breadth of mathematical tools applicable to such puzzles. The absence of a straightforward answer encourages creative exploration and the application of different mathematical concepts.
Approach 3: Base Conversion and Number Systems
A more advanced approach involves considering different number systems. Is it possible that the sequence is written in a non-decimal base? Let's explore this possibility:
-
Binary: Converting the numbers to binary, we get: 3 (11), 4 (100), 1 (1), 2 (10). No obvious pattern emerges from this conversion.
-
Ternary: In the ternary system (base-3), we have: 3 (10), 4 (11), 1 (1), 2 (2). Again, no immediate pattern is apparent.
-
Other Bases: Exploring other bases (quaternary, quinary, etc.) would require a systematic approach, potentially utilizing programming tools to automate the conversion and pattern recognition.
This exploration showcases the importance of considering different mathematical representations and the potential for hidden patterns to become visible when viewed through a different lens. The lack of an immediately apparent solution in standard base-10 further underlines the need for creativity and exploration of alternative systems.
Approach 4: Geometric or Spatial Interpretations
Perhaps the sequence represents spatial relationships or geometric patterns. We could consider:
-
Coordinates: Could the numbers represent coordinates on a plane? (3,4) and (1,2) would represent two distinct points. The relationship between these points (distance, angle, etc.) could provide clues to the pattern.
-
Shapes: Could the numbers relate to the properties of geometric shapes (number of sides, angles, area, etc.)? This approach requires a leap of imagination, connecting numerical sequences to visual representations.
Such geometric interpretations emphasize the multi-faceted nature of mathematical problem-solving, illustrating how seemingly abstract numerical sequences can be connected to visual representations. This interdisciplinary approach is crucial in complex problem-solving.
The Importance of Context and Further Information
It's critical to acknowledge that without additional context or information, a definitive solution to the "3, 4, in 1, 2" puzzle remains elusive. The ambiguity of "in" allows for multiple interpretations, making it a puzzle more about creative thinking and exploring different mathematical avenues than finding a single, universally accepted solution.
Imagine if the problem was presented as part of a larger context: a word puzzle, a riddle within a story, or a code in a larger cryptographic sequence. Such context could drastically alter our interpretation of "in" and guide us towards a specific solution.
This underscores a crucial principle in mathematics and problem-solving: the importance of context. The same numbers or sequence can mean different things depending on the context they are presented within.
Developing Problem-Solving Skills
The "3, 4, in 1, 2" puzzle, despite its lack of a single definitive answer, provides invaluable practice in developing critical thinking and problem-solving skills. The exercise helps in:
-
Creative Thinking: Exploring multiple interpretations and approaches pushes the boundaries of conventional thinking.
-
Pattern Recognition: Attempting to identify underlying patterns, even in the absence of an obvious one, sharpens pattern-recognition skills.
-
Mathematical Exploration: The puzzle encourages the application of various mathematical concepts and tools, fostering a deeper understanding of their applicability.
-
Logical Reasoning: Evaluating the validity of different interpretations and their consistency with the given data strengthens logical reasoning abilities.
Conclusion: Embracing the Ambiguity
The beauty of the "3, 4, in 1, 2" puzzle lies in its ambiguity. It's not a puzzle with a single right answer; instead, it's a journey of exploration, a testament to the creative potential of mathematical thinking. By embracing the ambiguity, we develop crucial problem-solving skills transferable to numerous fields. The process of exploration, of considering multiple interpretations and applying diverse mathematical tools, is as valuable as finding a definitive answer. This puzzle serves as a reminder that mathematical exploration is often as much about the journey as the destination. The true value lies in the development of critical thinking and creative problem-solving skills that emerge from the process. This seemingly simple sequence can become a gateway to a deeper appreciation of the power and beauty of mathematics.
Latest Posts
Latest Posts
-
Does New Zealand Have Spiders
Sep 12, 2025
-
Where Is Ibiza Island Located
Sep 12, 2025
-
San Diego California January Weather
Sep 12, 2025
-
Accommodation Near Kings Cross London
Sep 12, 2025
-
Does Fly Spray Kill Wasps
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 4 In 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.